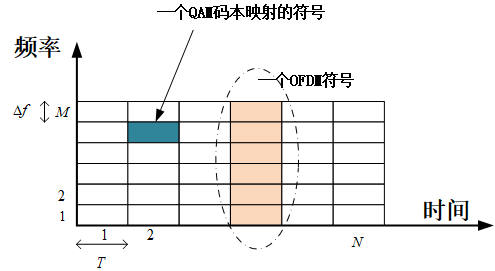
OFDM allows data to be transmitted on parallel channels as long as the orthogonality of subcarriers is not disrupted by the wireless channel.
The orthogonality property enables the use of a single tap equalizer to detect the transmitted data at the receiver.
发送端
image-20240624101346856 信道
OFDM_static_multi_paths_Channel 利用特征值分解有H = F H D F \bf H=F^HDF H = F H DF D = d i a g [ D F T M ( h ) ] \mathbf{D}=diag[DFT_M(\mathbf{h})] D = d ia g [ D F T M ( h )]
接收端
s ( t ) = ∑ n = 0 N − 1 ∑ m = 0 M − 1 X [ m , n ] g t x ( t − n T ) e j 2 π m Δ f ( t − n T ) g t x ( t ) = 1 , 0 ≤ t < T T = 1 / Δ f s(t)=\sum^{N-1}_{n=0}\sum^{M-1}_{m=0}\mathbf{X}[m,n]g_{tx}(t-nT)e^{j2\pi m\Delta f(t-nT)}\\ g_{tx}(t)=1, 0\leq t<T \\ T=1/\Delta f s ( t ) = n = 0 ∑ N − 1 m = 0 ∑ M − 1 X [ m , n ] g t x ( t − n T ) e j 2 πm Δ f ( t − n T ) g t x ( t ) = 1 , 0 ≤ t < T T = 1/Δ f
r = H s + w = F M ∗ D F M ⋅ s + w y = F M r = D x + w ^ , x = F M ⋅ s \mathbf{r=Hs+w=F_M^*DF_{M}\cdot s+w} \\ \mathbf{y=F_{M}r=Dx+\hat w,x=F_{M}\cdot s} r = Hs + w = F M ∗ D F M ⋅ s + w y = F M r = Dx + w ^ , x = F M ⋅ s
image-20240624104146740 符号检测
针对接收到的OFDM符号块中的一列,也即单个OFDM符号,使用single tap equalizer
x ^ = D A ( D − 1 y ) \mathbf{\hat x=\mathcal{D}_{A}(D^{-1}y)} x ^ = D A ( D − 1 y )
D A \mathcal{D}_A D A
信道估计
Assuming the channel is static over multiple OFDM symbols, the channel coefficients h [ m ] , m = 0 , . . . , M − 1 \mathbf{h}[m], m = 0,...,M − 1 h [ m ] , m = 0 , ... , M − 1 y [ m ] y[m] y [ m ] x = 1 M × 1 \mathbf{x} = \mathbf{1}_{M×1} x = 1 M × 1
OFDM enables a low complexity modulation and demodulation thanks to the FFT and the CP.(对于多载波调制技术而言)
高PAPR
P A P R d B \buildrel Δ = 10 log 10 max { ∣ s [ m ] ∣ 2 } E { ∣ s [ m ] ∣ 2 } , m = 0 , ⋯ , M − 1 PAP{R_{dB}} \buildrel \Delta \over = 10{\log _{10}}\frac{{\max \{ {{\left| {{\bf{s}}[m]} \right|}^2}\} }}{{E\{ {{\left| {{\bf{s}}[m]} \right|}^2}\} }},m = 0, \cdots ,M - 1 = 10 log 10 E { ∣ s [ m ] ∣ 2 } m a x { ∣ s [ m ] ∣ 2 } , m = 0 , ⋯ , M − 1 P A P R d B \buildrel Δ
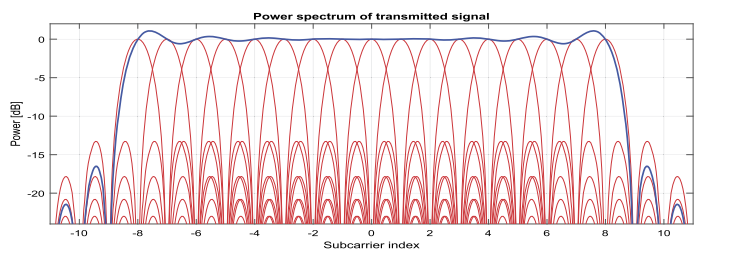
高 OOB(out-of_band,带外发射)
S ( w ^ ) = ∑ m = 0 M − 1 H m ( w ^ ) S X [ m ] ( w ^ ) H m ( w ^ ) = s i n ( M ( w ^ 2 − π m M ) ) M s i n ( w ^ 2 − π m M ) S(\hat w)=\sum^{M-1}_{m=0}H_m(\hat w)S_{\bf{X}[m]}(\hat w) \\ H_m(\hat w)=\frac {sin(M(\frac{\hat w}{2}-\frac{\pi m}{M}))}{Msin(\frac{\hat w}{2}-\frac{\pi m}{M})} S ( w ^ ) = m = 0 ∑ M − 1 H m ( w ^ ) S X [ m ] ( w ^ ) H m ( w ^ ) = M s in ( 2 w ^ − M πm ) s in ( M ( 2 w ^ − M πm ))
对于载波频偏敏感
定义频偏
f o = f c − f c ′ f_o=f_c -f'_c \\ f o = f c − f c ′
频偏的归一化
ε = f o Δ f = ⌊ ε ⌋ + Δ ε \varepsilon = \frac{{{f_o}}}{{\Delta f}} = \left\lfloor \varepsilon \right\rfloor + \Delta \varepsilon ε = Δ f f o = ⌊ ε ⌋ + Δ ε
无噪声条件下
y c f o = C D x \mathbf{y}^{cfo}=\mathbf{CDx} y c f o = CDx
C { m , m ′ } = s i n ( π ( m − m ′ + ε ) ) M s i n ( π ( m − m ′ + ε ) M ) e j π ( m − m ′ + ε ) ( M − 1 ) M , m , m ′ ∈ [ 0 , M − 1 ] \mathbf{C}_{\{m,m'\}}=\frac{sin(\pi(m-m'+\varepsilon))}{Msin(\frac{\pi(m-m'+\varepsilon)}{M})}e^{\frac{j\pi(m-m'+\varepsilon)(M-1)}{M}},m,m'\in [0,M-1] C { m , m ′ } = M s in ( M π ( m − m ′ + ε ) ) s in ( π ( m − m ′ + ε )) e M jπ ( m − m ′ + ε ) ( M − 1 ) , m , m ′ ∈ [ 0 , M − 1 ]
当观察m = m ′ m=m' m = m ′
**载波频偏补偿方法:**先利用导频估计f o f_o f o e − j 2 π f ^ 0 t e^{-j2\pi \hat f_0 t} e − j 2 π f ^ 0 t